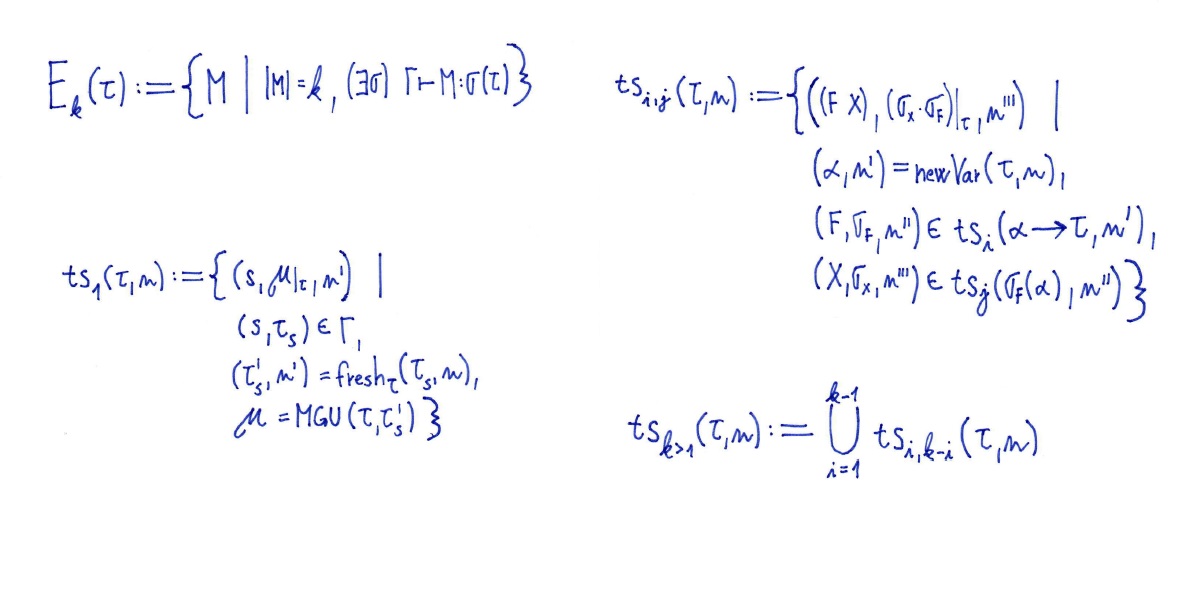In this paper we describe a multi-objective genetic programming algorithm which can be used to create complete machine learning workflows. The algorithm is an extension of a single-objective one. In a series of test on four datasets, we show that the additional objectives can be used to search for smaller or faster models. The algorithm is also in some cases much faster than the single-objective one while obtaining results of similar quality.

Automated program discovery has been mainly approached via Genetic Programming, which represents the search space of programs implicitly by a collection of individuals. In this paper, we propose a way of representing program search space explicitly, with a top-down hierarchy of semi-constructed programs. Together with a bottom-up generation procedure, we maintain an overview of the overall search space structure, while being able to quickly get samples from the fringe. Moreover, having a type system with parametric polymorphism allows us to limit the state space size using type level programming while keeping a complete control over program sizes. Our approach can naturally be used for searching the space of programs using tree search methods. We back this claim by a simple experiment utilizing a Monte-Carlo Tree Search algorithm, though other search methods (such as A*) might be used as well.

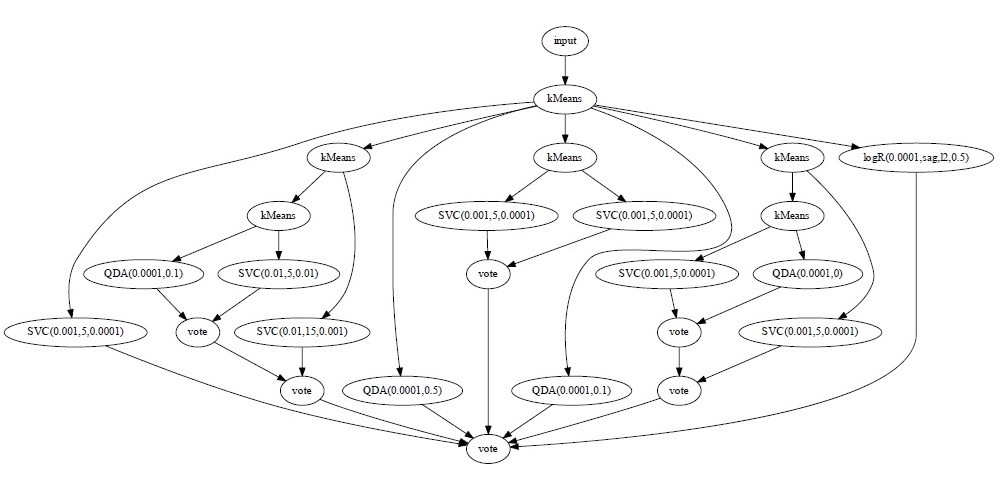
Manual creation of machine learning ensembles is a hard and tedious task which requires an expert and a lot of time. In this work we describe a new version of the GP-ML algorithm which uses genetic programming to create machine learning workflows (combinations of preprocessing, classification, and ensembles) automatically, using strongly typed genetic programming and asynchronous evolution. The current version improves the way in which the individuals in the genetic programming are created and allows for much larger workflows. Additionally, we added new machine learning methods. The algorithm is compared to the grid search of the base methods and to its previous versions on a set of problems from the UCI machine learning repository.

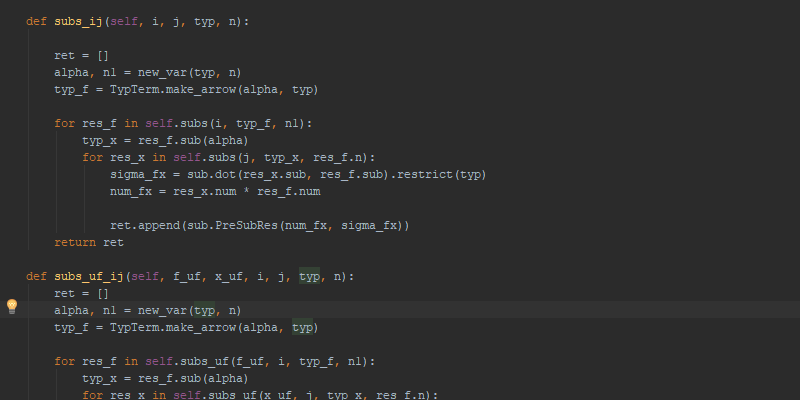
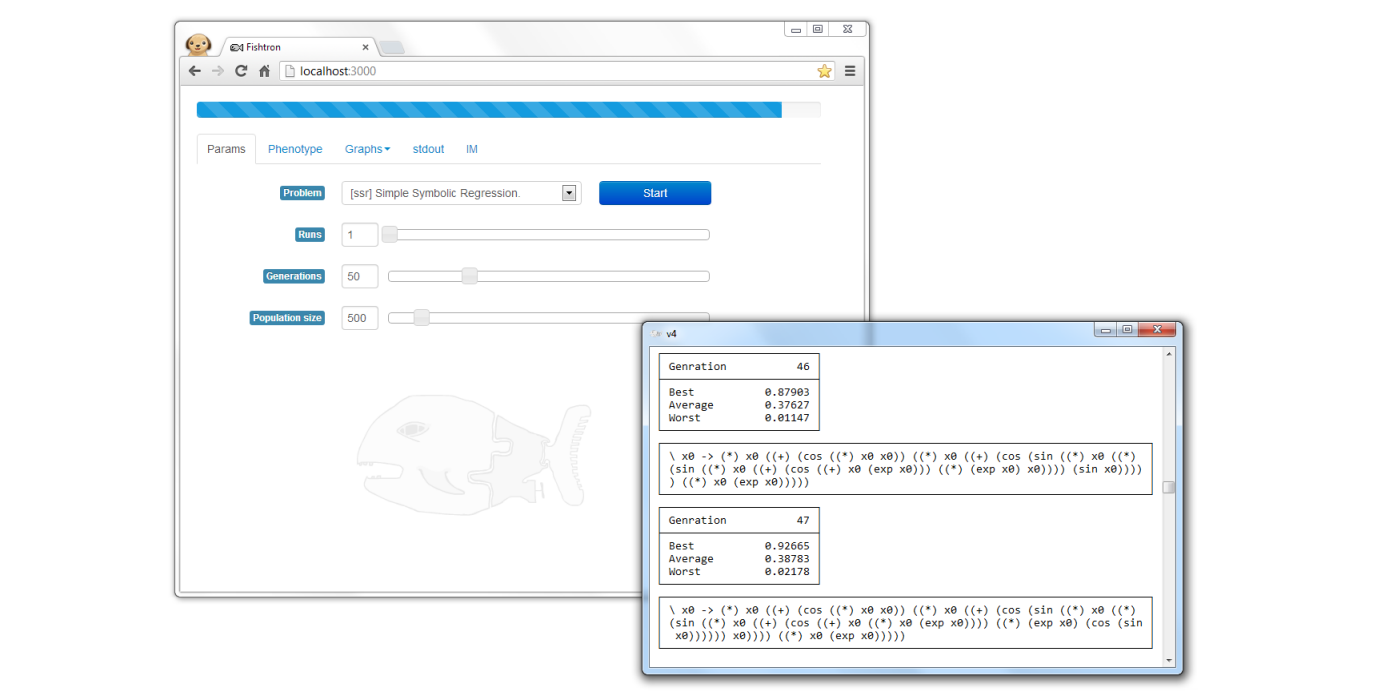
In this paper we present a new initialization method for genetic programming based on randomized exhaustive enumeration. It naturally enables complete sharing of sub trees among individuals which in turn allows an efficient reuse of computations. Moreover, it can be implemented as a random one pass initialization. We present experimental results on different instances of simple symbolic regression exploring the landscape of possible initializations based on our approach and confirming the usability of these initializations.

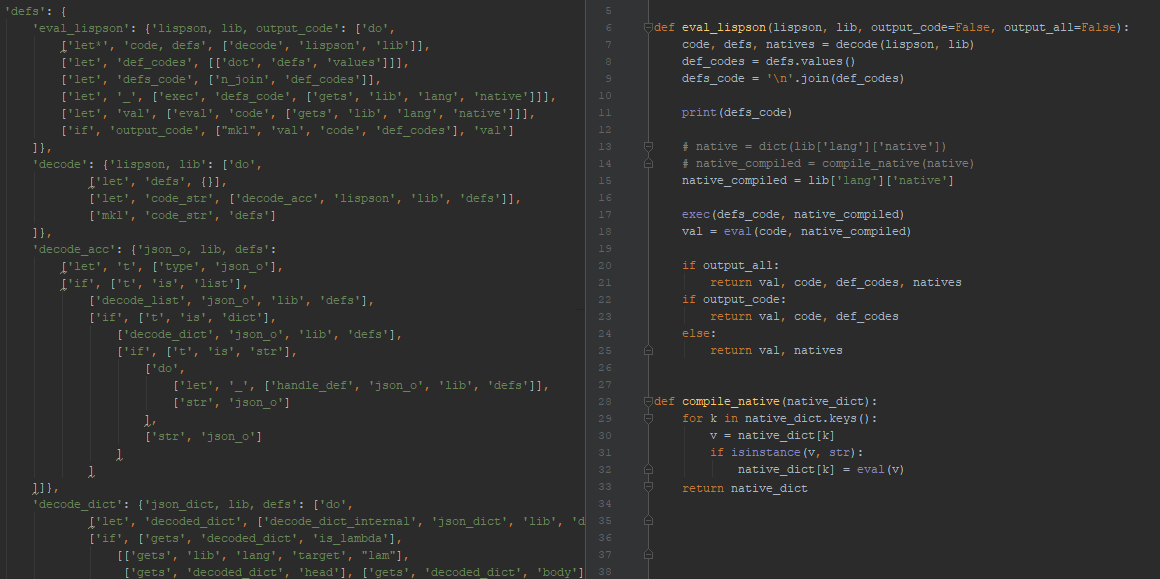
Lambda calculus representation of programs offers a more expressive alternative to traditional S-expressions. In this paper we discuss advantages of this representation coming from the use of reductions (beta and eta) and a way to overcome disadvantages caused by variables occurring in the programs by use of the abstraction elimination algorithm. We discuss the role of those reductions in the process of generating initial population and propose two novel crossover operations based on abstraction elimination capable of handling general form of typed lambda term while being a straight generalization of the standard crossover operation. We compare their performances using the even parity benchmark problem.

Tree based genetic programming (GP) traditionally uses simple S-expressions to represent programs, however more expressive representations, such as lambda calculus, can exhibit better results while being better suited for typed GP. In this paper we present population initialization methods within a framework of GP over simply typed lambda calculus that can be also used in the standard GP approach. Initializations can be parameterized by different search strategies, leading to wide spectrum of methods corresponding to standard ramped half-and-half initialization on one hand, or exhaustive systematic search on the other. A novel geometric strategy is proposed that balances those two approaches. Experiments on well known benchmark problems show that the geometric strategy outperforms the standard generating method in success rate, best fitness value, time consumption and average individual size.